Конспект лекции: Способы коррекции и компенсации погрешностей аналоговых измерительных устройств

Существуют следующие способы:

• 1) Калибровка.
• 2) Аддитивная коррекция.
• 3) Мультипликативная коррекция.
• 4) Автоматическая коррекция способом итераций.
• 5) Способ образцовых сигналов.

Структурная схема калибровки:

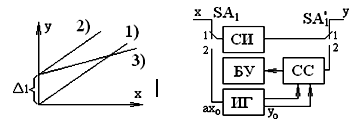
1) ах=у.
2) у=ах+Δ₁, х=0, у≠0.
3) у=(а+Δ₂)х+Δ₁. Δ₁ и Δ₂ - аддитивная и мультипликативная погрешности СИ.

БУ - блок управления, СС - схема сравнения, ИГ - измерительный генератор, SA₁ и SA₁^′ - переключатели.

При переключении SA₁ и SA₁^′ в положение 2 осуществляется калибровка. На вход СИ с СС подаётся нулевой сигнал, тогда у=Δ₁=у^′, т.е. на выходе СС появляется сигнал у^′=Δ₁. При наличии аддитивной погрешности Δ₁ блок БУ изменяет параметры СИ, устраняя эту погрешность установлением нулевого выходного сигнала СИ и у=(а+Δ₂)·х, затем на вход СИ подаётся сигнал х₀, а на вход СС - у₀. Тогда у₀=(а+Δ₂)·х₀, далее с помощью БУ или вручную регулируется передаточный коэффициент СИ до величины а^′= а-Δ₂ путём установления на выходе сигнала равного у₀. Затем переключатели переводятся в положение 1 и на вход СИ поступает измеряемый сигнал. В этом случае выходной сигнал в статике будет равен выходному сигналу идеального СИ с точностью до погрешностей калибровки. у=(а-Δ₂+Δ₂)х=ах.

Аддитивная коррекция:

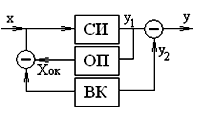
При данном способе коррекции уменьшение погрешностей осуществляется за счёт смещения функции преобразования СИ. ОП - обратный преобразователь (образцовый). Используется для выявления погрешностей. Операция выявления сигнала погрешности Δх происходит в результате одновременного или равномерного вычитания 2-х сигналов. Усиленный вспомогательным каналом ВК разностный сигнал у₂ используется для введения поправки СИ. Пусть СИ имеет аддитивную и мультипликативную погрешность и его выходной сигнал у₁=(а+Δ₂)х+Δ₁. А образцовый преобразователь имеет идеальную передаточную характеристику вида:

Х_ок=1/а·у₁=1/а·((а+Δ₂)х+Δ₁)=х+(Δ₂х/а)+Δ₁/а.
Δх=Х-Х_ок==-(Δ₁/а+Δ₂/а·х).
у=у₁-у₂=(а+Δ₂)х+Δ₁-а^′(-Δ₁/а+Δ₂/а·х)=х(а+Δ₂(1-а^′/а))+Δ₁(1-а^′/а).

Если а^′=а, то корректируется аддитивная составляющая.

Мультипликативная коррекция.

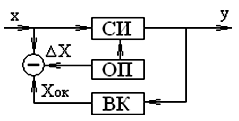
В СИ с мультипликативной коррекцией погрешностей осуществляется выделение погрешностей СИ и управление его коэффициентом преобразования СИ для минимизации этой погрешности. Таким способом можно корректировать аддитивные и мультипликативные погрешности, однако при преобладании аддитивной погрешности коррекция осуществляется лишь в одной точке шкалы СИ.

Пусть характеристика преобразования такого СИ имеет вид:

у=(а+кz)к+Δ₁,
где кz - изменение коэффициента преобразования Си от действия сигнала z.

Запишем:

у_н=а_ном·х.
Δу=у-у_н=(а+кz-а_ном)х+Δ₁.
Х_ок=(1/а_ном)х=(1/а_ном)(а+кz)х+Δ₁/а_ном.
Δх=х-Х_ок=х-(1/а_ном)(а+кz)х-Δ₁/а_ном.
z=К_номΔх+Δх₁^′+Δх₂^′Δх.

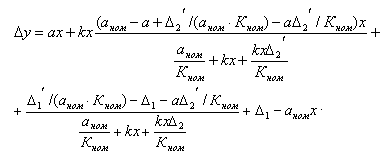
Из соотношения видно, что при К_ном→∞, Δу=0, т.е. для снижения погрешности СИ необходимо увеличить коэффициент передачи вспомогательного канала ВК.

Автоматическая коррекция способом итераций.

Использование этого способа в ряде случаев позволяет свести точность измерения с помощью АЭП к точности использования образцовой меры.

Способ образцовых сигналов.

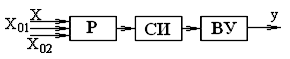
Для практической реализации способа необходимо иметь избыточность по быстродействию и набор образцовых сигналов. Где Р - включ. поочерёдно к входу образцовых значений х, СИ - система измерения, ВУ - вычислительное устройство. В случае линейного СИ можно записать для:

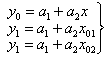
Где а₁ и а₂ - коэффициенты характеристики преобразования СИ. Решив систему уравнений получим: х=х₀₂(у₀-у₁)/(у₂-у₁)-х₀₁(у₂-у₀)/(у₂-у₁). Видно, что значение х не зависит от изменения параметров характеристики преобразования. Таким образом, снижается как аддитивная так и мультипликативная составляющие погрешности. Это даёт хорошие результаты, когда значения х и коэффициентов а₁ и а₂ не изменяются за время, необходимое для получения одного результата измерения.

Компенсация погрешностей.

В АЭП компенсация погрешностей производится способом составных параметров и компенсирующего преобразования с полной и неполной компенсацией.

Внимание! Каждый электронный конспект лекций является интеллектуальной собственностью своего автора и опубликован на сайте исключительно в ознакомительных целях.