Конспект лекции: Статические погрешности ЦИП

Статические погрешности складываются обычно из следующих составляющих:

• - погрешность дискретности ΔX_A;
• - погрешность реализации уровней квантования ΔX_Р, возникающей от несоответствия принятых значений уровней квантования и их реальных значений;
• - погрешность ΔX₄ от наличия порога чувствительности или от нестабильности порога чувствительности сравнивающего устройства;
• - погрешность ΔX_П от действия помех на ЦИП и его элементы.

Составляющие ΔX_Р, ΔX₄ и ΔX_П обусловлены несовершенством прибора и поэтому они называются составляющими инструментальной погрешности. Погрешность дискретности – методическая погрешность.

Рассмотрим погрешность дискретности при различных способах отождествления уровня квантования. Для упрощения анализа положим, что ΔX_Р=0, ΔX₄=0, ΔX_П=0.

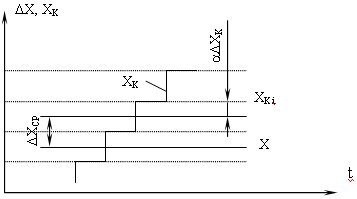
Погрешность дискретности при разных способах отождествления можно рассмотреть на примере прибора последовательного счета, в котором измеряемая величина X сравнивается с известной величиной ΔX_К , изменяющейся во времени скачками в один квант:

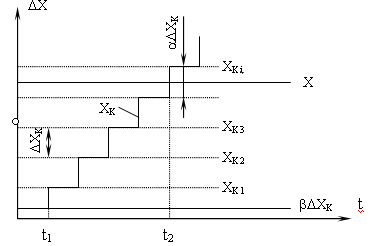
Последовательно с источником X_К включен источник βX_К. Определение отождествляемого уровня происходит при установлении равенства X_К и X или, точнее, при выполнении условия: (X_Кi + βΔX_К )>=X

Показания прибора должны устанавливаться в соответствии с отождествляемым, т.е. в данном случае с уровнем X_Кi. Номер отождествляемого уровня, а следовательно и погрешность прибора зависят от значений Х и β.

После фиксации равенства X_К и Х в момент t₂ установится соотношение:

(X_Кi + βΔX_К)-X=αΔX_K, где
α - случайный безразмерный коэффициент, принимающий при повторных измерениях значение в пределах от 0 до 1.

Погрешность прибора при этом будет:

ΔX=X_Кi - X = αΔX_K - βΔX_К

В полученной погрешности можно выделить две составляющие:

• - случайную ΔX_Д = αΔX_К - ΔX_K/2 ;
• - систематическую ΔX_К/2 - βΔX_К

Случайная составляющая ΔX_Д носит название погрешности дискретности (квантования).

Таким образом, при указанных условиях погрешность прибора:

ΔX = (αΔX_K - ΔX_K/2) + (ΔX_K/2 - βΔX_К) = ΔX_Д + (ΔX_K/2 - βΔX_К)

Значения погрешности дискретности лежат в пределах от - ΔX_K/2 до ΔX_K/2. В силу равной вероятности появления любого значения измеряемой величины в пределах одного шага квантования дифференциальный закон распределения погрешности дискретности принимается равномерным в пределах от - ΔX_K/2 до ΔX_K/2. Следовательно, среднеквадратическое отклонение погрешности дискретности:

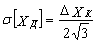
Изменение βΔX_К ведет к изменению способа отождествления и, следовательно, к изменению систематической составляющей погрешности прибора. Действительно, при β=0 систематическая составляющая погрешности прибора М[ΔX]= ΔX_К/2 , что соответствует отождествлению с ближайшим большим по значению или равным уровнем квантования.

При β=1 имеем М[ΔX] = - ΔX_К/2, что соответствует отождествлению с ближайшим меньшим по значению или равным уровнем квантования. При β=0,5 имеем М[ΔX]=0, что соответствует отождествлению с ближайшим по значению уровнем квантования.

В самом общем случае при 0 <= β <= 1 имеем М[ΔX]=(0,5-β)ΔX_К и при этом отождествление происходит с ближайшим большим или с ближайшим меньшим или равным по значению уровнем квантования.

На рисунке показана зависимость погрешности прибора от измеряемой величины для разных значений β:

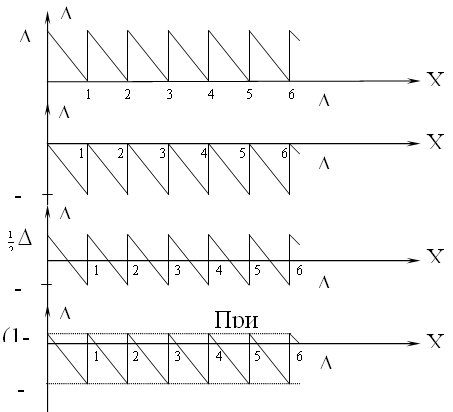
Периодический характер погрешности придает периодическая зависимость α=f(x). На рисунке также видна зависимость систематической составляющей от β (от способа отождествления). Из приведенных выражений и рисунка следует, что для уменьшения погрешности прибора необходимо стремиться к отождествлению с ближайшим уровнем квантования, но погрешность прибора не может быть меньше погрешности дискретности.

Для определения влияния порога чувствительности Х₄ сравнивающего устройства СУ примем ΔХ_Р=0, ΔХ_П=0, Х=const и будем считать, что величина Х_К возрастает во времени скачками в один квант и срабатывание СУ происходит при X_Кi >= X+X_СР

В этом случае погрешность прибора

ΔX = X_Кi – Х = αΔX_K + X_СР = (α&DeltaX_K - ΔX_К/2)+(ΔX_K/2+X_СР), где &alpha=0 .. 1

Как видно, погрешность ΔХ имеет две составляющие, из которых первая (αΔX_K -ΔX_К/2) – погрешность дискретности, а вторая – систематическая, зависящая от порога чувствительности СУ. Для уменьшения систематической составляющей применяют СУ с X_СР → 0 или последовательно с Х_К вводят дополнительный сигнал, равный X_СР + ΔX_K/2 . В последнем случае систематическая составляющая будет равна нулю.

Рассмотрим погрешности, возникающие в ЦИП при квантовании временного интервала. Временной интервал t_x в ЦИП измеряется путем подачи числа квантующих импульсов стабильной частоты f₀=1/T₀, прошедших в счетчик импульсов за время t_x.

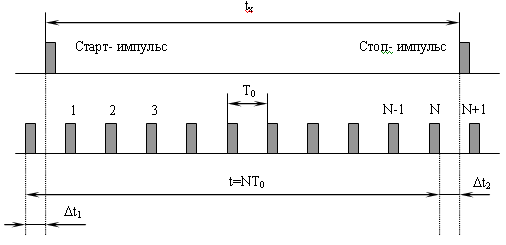
В общем случае t_x не кратно Т₀ и поэтому возникает погрешность Δt = t - t_x , где t=NT₀ (N- число импульсов, зафиксированных счетчиком импульсов). Эта погрешность зависит от временного сдвига старт- и стоп- импульсов относительно квантующих импульсов и выражается в виде двух составляющих Δt = Δt₁ - Δt₂ =α₁T₀ - α₂T₀, где α₁=0..1 и α₂=0..1 - случайные коэффициенты.

Первая составляющая Δt₁=α₁T₀ называется погрешностью от случайного расположения начала шкалы. Она всегда находится в пределах 0..Т₀ и имеет равномерный дифференциальный закон распределения, так как появление старт- импульса между квантующими импульсами равновероятно. Вторая составляющая Δt₂=α₂T₀ – погрешность, вызванная случайным расположением стоп- импульса относительно квантующих импульсов и соответствующая отождествлению с ближайшим меньшим или равным уровнем квантования. Дифференциальный закон распределения этой погрешности – равномерный в пределах –Т₀..0.

Результирующая предельная погрешность Δt_m=±T₀ ; относительная результирующая предельная погрешность:

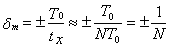
Закон распределения результирующей погрешности определяется как композиция законов распределения двух указанных составляющих и является распределением Симпсона (треугольным) в пределах -Т₀..+Т₀. Среднеквадратическое отклонение и систематическая составляющая результирующей погрешности соответственно равны:

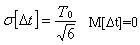
Предельные значения и среднеквадратическое отклонение результирующей погрешности снижаются синхронизацией стартового и квантующего импульсов со сдвигом T₀/2, т.е. путем расположения стартового импульса в середине между двумя соседними квантующими импульсами. В этом случае Δt₁=T₀/2 и Δt=T₀/2 - α₂T₀ , а предельные значения, среднеквадратическое отклонение и систематическая составляющая результирующей погрешности соответственно равны:

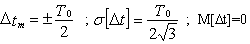
Дополнительные погрешности ЦИП, также как и в аналоговых приборах, возни-кают при изменении внешних факторов (температуры, напряжения и частоты источника питания, действия помех и т. д.).

Внимание! Каждый электронный конспект лекций является интеллектуальной собственностью своего автора и опубликован на сайте исключительно в ознакомительных целях.