Конспект лекции: Цифровое измерение интервалов времени (функциональная схема, диаграмма работы, погрешности)
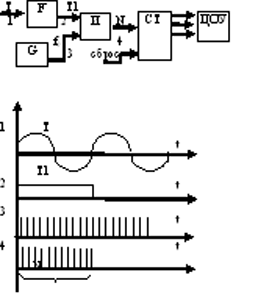
Это приборы, предназначенные для измерения для различных промежутков времени с представлением результата измерения в цифровой форме. К ним относятся:
- 1) измеритель периода периодического сигнала (Т);
- 2) измеритель длительности импульса (τ);
- 3) измеритель интервала времени (t).
Все ЦХ основаны на времяимпульсном преобразовании.
Количество импульсов, поступающих на счетчик будет равно: N=T/T0=T*f0. Отсюда следует, что Т=N/f0=g*N – дискретное значение периода. В этой схеме те же источники погрешностей, что и для ЦЧ, поэтому относительная погрешность ЦХ будет δ=ΔT/T=±( δf0+1/(f0*T)).
Этот прибор позволяет измерять и частоту, то есть f=1/T.
В отличие от предыдущей схемы (ЦЧ) в данном случае вторая составляющая 1/(f0*T) уменьшается с ростом Т, т.е. при уменьшении f. Следовательно, этот прибор можно использовать для измерения низких частот. При уменьшении периода вторая составляющая погрешности растет. Этот рост можно уменьшить, используя делитель частоты. Тогда:
N=k*T/T0=k*f0*T;
T=N/(k*f0)=g*N;
δ=±( δf0+1/(f0*T*k)).
С целью дальнейшего уменьшения погрешности дискретности при измерении перода производят измерения среднего из n периодов. В связи с этим деление осуществляется переносом запятой или сменой единиц измерения (Герц, килоГерц, Мега Герц). При измерении из n периодов относительная погрешность будет равна:
- а) для синусоидального сигнала ±δf0+δф/n+1/(n*t*f0), где δф=1/π*Uп/Uс, где Uп и Uс – амплитуды помехи и полезного сигнала, соответственно.
- б) для импульсных сигналов δ=±( δf0+1/(f0*T*n)).
Обычно погрешность дискретности δД=(0,3-0,5)*δ, тогда δД=1/(Т*f0)<=(0,3–0,7)*δ. Следовательно f0<=1/(Tmin*(0,3 – 0,7)*δ) – частота задающего генератора.
Дом на берегу волги купить в Нижегородской области купить дом у реки в Нижегородской области.
Внимание! Каждый электронный конспект лекций является интеллектуальной собственностью своего автора и опубликован на сайте исключительно в ознакомительных целях.