Конспект лекции: Свойства и нотации преобразований Фурье.
Нотации преобразования Фурье. Часто пользуются записью спектра в полярной нотации, т.е. в виде только амплитуд и начальных фаз одних только косинусоид. Наиболее понятна полярная запись, т.е. в виде спектра амплитуд и спектра фаз. Спектр амплитуд показывает распределение энергии по частотам. Спектр фаз говорит о временных характеристиках сигналов. Чаще всего спектр фаз используется в тех областях, где нужно исследовать задержки и длительности импульсов. Прямоугольная нотация более удобна для вычислительных операций. При вычислении спектра дискретных сигналов получают массив, состоящий из комплексных чисел. Этот массив имеет размерность в 2 раза меньшую, чем исходный временный массив. Общее количество информации остаётся неизменным. Обратное преобразование Фурье даёт исходный массив. В частотном массиве содержаться значения для частот от 0 до частоты Найквиста. Для аналоговых сигналов такого ограничения не существует.
Свойства преобразований Фурье.
1) Преобразование Фурье является линейной операцией, т.к. обладает свойством гомогенности и аддитивности.
2) Аддитивность – сложение 2-х сигналов вызывает сложение их спектров и наоборот.
3) Смещение сигнала во времени никак не влияет на спектр амплитуд, зато к функции спектра фаз необходимо прибавить произведение Δt*ω, где Δt – смещение во времени. Спектр фаз несёт информацию о временной задержке, длительности импульса. Смещение импульса во времени вызывает изменение спектра фаз. Один и тот же интервал времени на разных частотах представляет собой разный сдвиг фаз. Обратное преобразование Фурье с использованием одного только спектра фаз даёт возможность увидеть только временные характеристики исходного сигнала.
4) Преобразование Фурье симметрично относительно нуля времени и нуля частоты.
5) Перемножение сигнала на некоторый гармонический тон вызывает амплитудную модуляцию. Спектр исходного сигнала смещается на частоту несущей. Получаются 2 боковые полосы.
DSB (амплитудная модуляция без несущей):
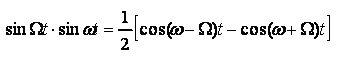
Ω<<ω, ω - частота несущей
АМ (амплитудная модуляция с несущей):
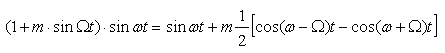
sin(ωt) - несущая, m - глубина модуляции (коэффициент)
Перемножение 2-х сигналов – нелинейная операция, поскольку не обладает частотной верностью.
Быстрое преобразование Фурье (БПФ). Это алгоритм, предназначенный для вычисления спектров дискретных сигналов. Для своей реализации требует существенно меньше вычислительных операций. БПФ может работать только с сигналами длинной 2n выборок. Также существует и обратное преобразование Фурье.
Внимание! Каждый электронный конспект лекций является интеллектуальной собственностью своего автора и опубликован на сайте исключительно в ознакомительных целях.