Конспект лекции: Корреляция, автокорреляция, взаимная корреляция. Свойства автокорреляционной и взаимной корреляционной функции

Корреляция – математическая операция, схожа со свёрткой, позволяет получить из двух сигналов третий. Бывает: автокорреляция (автокорреляционная функция), взаимная корреляция (взаимнокорреляционная функция, кросскорреляционная функция). Пример:

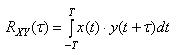[Взаимная корреляционная функция]

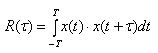[Автокорреляционная функция]

Корреляция - это техника обнаружения заранее известных сигналов на фоне шумов, ещё называют оптимальной фильтрацией. Хотя корреляция очень похожа на свёртку, но вычисляются они по-разному. Области применения их также различные (c(t)=a(t)*b(t) - свертка двух функций, d(t)=a(t)*b(-t) - взаимная корреляция).

Корреляция – это та же свёртка, только один из сигналов инвертируется слева направо. Автокорреляция (автокорреляционная функция) характеризует степень связи между сигналом и его сдвинутой на τ копией. Взаимнокорреляционная функция характеризует степень связи между 2-мя разными сигналами.

Свойства автокорреляционной функции:

• 1) R(τ)=R(-τ). Функция R(τ) – является чётной.
• 2) Если х(t) – синусоидальная функция времени, то её автокорреляционная функция – косинусоидальная той же частоты. Информация о начальной фазе теряется. Если x(t)=A*sin(ωt+φ), то R(τ)=A²/2 * cos(ωτ).
• 3) Функция автокорреляции и спектра мощности связаны преобразованием Фурье.
• 4) Если х(t) – любая периодическая функция, то R(τ) для неё может быть представлена в виде суммы автокорреляционных функций от постоянной составляющей и от синусоидально изменяющейся составляющей.
• 5) Функция R(τ) не несёт никакой информации о начальных фазах гармонических составляющих сигнала.
• 6) Для случайной функции времени R(τ) быстро уменьшается с увеличением τ. Интервал времени, после которого R(τ) становится равным 0 называется интервалом автокорреляции.
• 7) Заданной x(t) соответствует вполне определённое R(τ), но для одной и той же R(τ) могут соответствовать различные функции x(t)

Исходный сигнал с шумами:

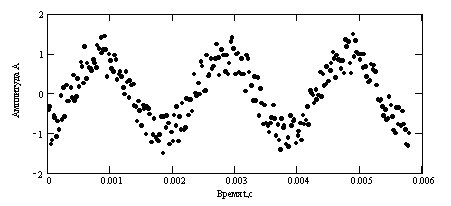
Автокорреляционная функция исходного сигнала:

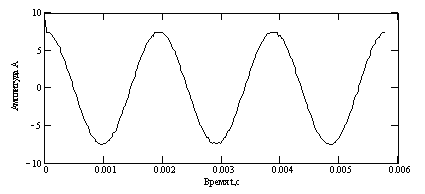
Свойства взаимной корреляционной функции (ВКФ):

• 1) ВКФ не является ни чётной ни нечётной функ¬цией, т.е. R_ху(τ) не равно R_ху(-τ).
• 2) ВКФ остаётся неизменной при перемене чередования функций и изменений знака аргумента, т.е. R_ху(τ)=R_ху(-τ).
• 3) Если случайные функции x(t) и y(t) не содержат постоянных составляющих и создаются независимыми источниками, то для них R_ху(τ) стремится к 0. Такие функции называются некоррелированными.

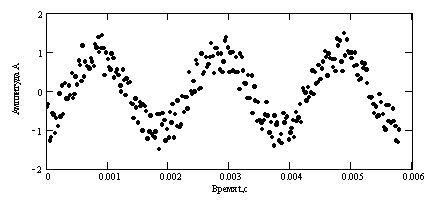
Исходный сигнал с шумами:

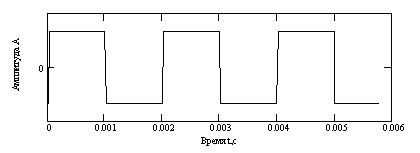
Меандр той же частоты:

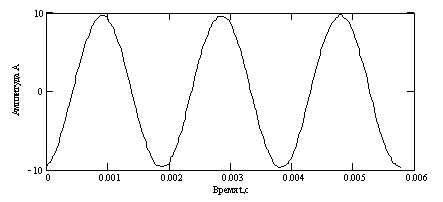
Корреляция исходного сигнала и меандра:

Внимание! Каждый электронный конспект лекций является интеллектуальной собственностью своего автора и опубликован на сайте исключительно в ознакомительных целях.