Конспект лекции: Сущность преобразования Лапласа

Преобразование Лапласа. Когда система описывается дифференциальными и интегральными уравнениями часто удобно воспользоваться преобразованием Лапласа для их расчёта. При этом уравнения становятся алгебраическими. При этом упрощённо можно считать ПЛ разложением сигнала на синусоиды и экспоненты. Для дискретных сигналов ПЛ называется Z-преобразованием.

Суть преобразования Лапласа

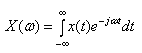- Преобразование Фурье

Различным функциям вещественых перемещений времени t ПЛ ставят в соответствие функции комплексного перемещения p и наоборот.

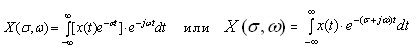- Преобразование Лапласа

р=σ+jω – оператор дифференцирования

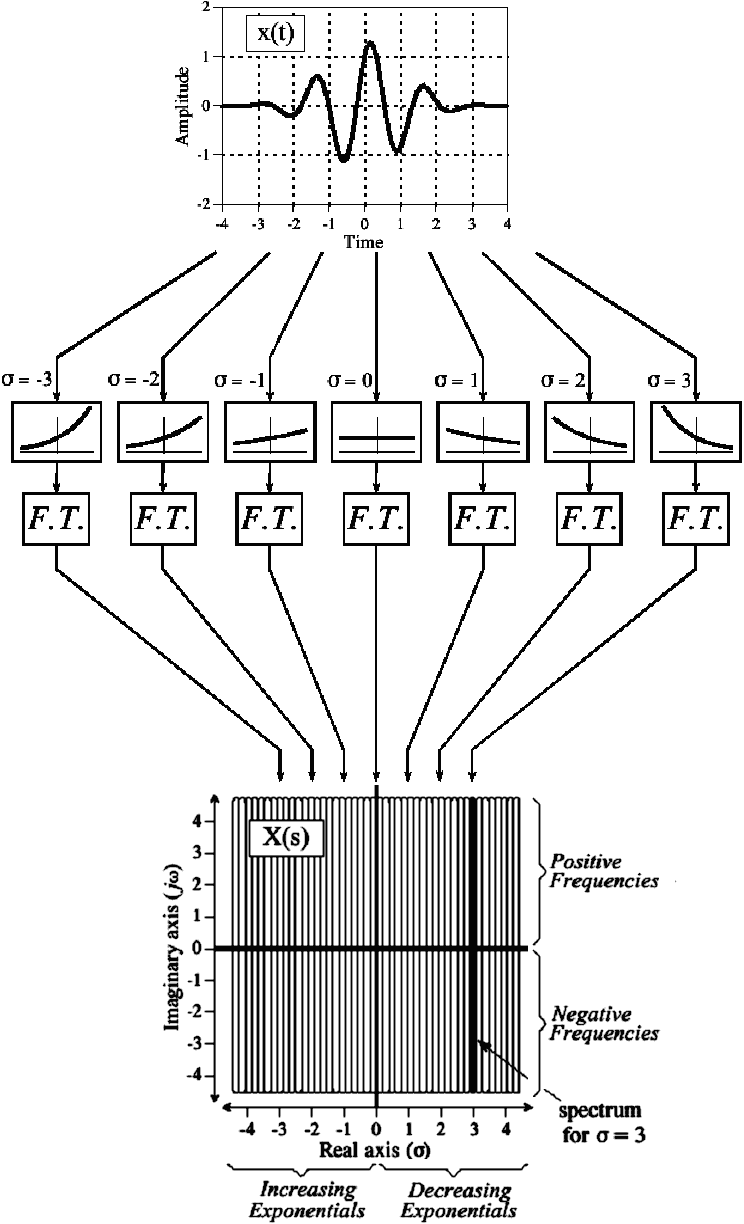
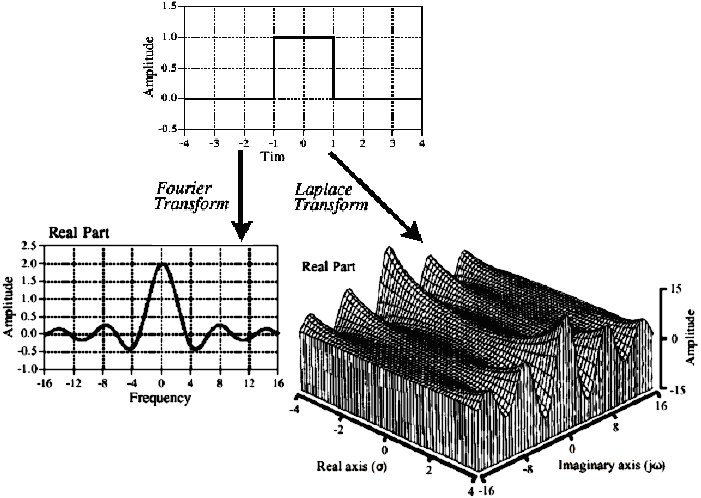
Изображение функции по Лапласу представляет собой комплексную плоскость, где по оси действительных значений отложено σ, по оси мнимых значений – величины jω. При этом каждая точка плоскости является величиной комплексной и может быть представлена в алгебраической или полярной нотации. Для того, чтобы найти изображение по Лапласу, исходный сигнал перемножают на различные экспоненты e^-σt. Если σ<0, то экспоненты возрастающие (левая полуплоскость), если σ>0, то правая полуплоскость. Для каждого из этих произведений находят преобразование Фурье и располагают вдоль оси мнимых значений. Верхняя и нижняя полуплоскости будут зеркальными, если исходный сигнал представлен действительной функцией.

Внимание! Каждый электронный конспект лекций является интеллектуальной собственностью своего автора и опубликован на сайте исключительно в ознакомительных целях.